Masala #0681

\(n\) ta tugundan iborat ildizga ega binar daraxt berilgan (rooted binary tree). Ya’ni daraxtning har bir tugunini ko’pi bilan ikkita bolasi bo’lishi mumkin.
Berilgan daraxtda iloji boricha ko’p tugunlarni bo’yash kerakki, bo’yalganidan so’ng daraxt muvozanatlangan bo’lib qolsin.

Muvozanatlangan daraxt deb quyidagi shartni qanoatlantiruvchi daraxtga aytiladi:
- har bir ikkita bolasi bor \(u\) tugun uchun, shu bolalarini \(x\) va \(y\) bilan belgilaydigan bo’lsak, ildizi \(x\) da bo’lgan va ildizi \(y\) da bo’lgan qism daraxtlardagi bo’yalgan tugunlar soni teng bo’lsin.

Masalan, quyidagi daraxt muvozanatlangan daraxtga misol bo’la oladi:

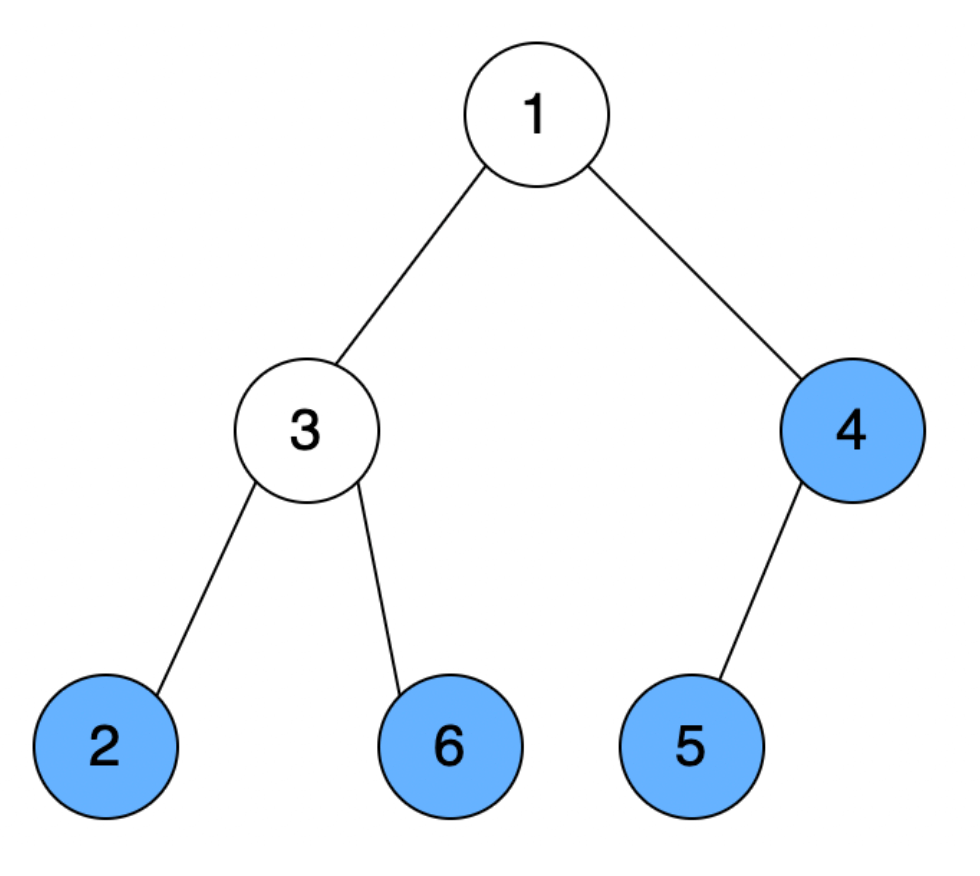
- 3-tugunni ikkala bolasidagi qism daraxtda 1 tadan bo’yalgan tugun bor.
- 1-tugunni ikkala bolasidagi qism daraxtda 2 tadan bo’yalgan tugun bor.
- 4-tugunni bolalari soni 1 ta bo’lgani sabab, uni e’tiborga olish shart emas.

Birinchi qatorda tugunlar soni \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda daraxt qirralarini ifodalovchi \(n - 1\) ta \(u\) va \(v\) ko’rinishidagi sonlar juftligi beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Daraxt ildizi doim 1-tugun bo’ladi.

1-subtask(9 ball): Har bir tugunning ko’pi bilan bitta bolasi bor, \(n ≤ 100\)
2-subtask(20 ball): \(n ≤ 15\)
3-subtask(31 ball): Har bir tugunning 0 ta yoki 2 ta bolasi bor \(n ≤ 10^5\)
4-subtask(40 ball): \(n ≤ 10^5\)

Bitta butun son - bo’yash mumkin bo’lgan maksimal tugunlar sonini chiqaring.